Bers Slice Project

1999年5月27日の記録

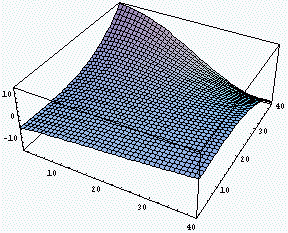
A^2のトレースの虚数部分のグラフ

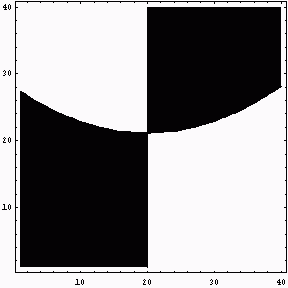
Aのトレースのreal locus （境界のところで、trace functionは零点を持っているのが見える）

1999年6月4日の記録

久々にMathematicaに触ってみる。（すっかりコマンドを忘れている。）とりあえず2時間ほどの空きが出来たので計算を始めるが、一応何本かのトレース函数のreal locusが計算出来た。求めるBers sliceは実軸及び虚軸に関して対称なので、どれか一つの象眼だけで考えれば十分である。というわけで、Farey数列で言えば、0/1と1/1の間にある分のreal locusだけを計算させてみた。
最初は1/2だ。うむ？！やけに短いぞ。（下の図では確かに一番短い線がそれです。）次は1/3だが、ちょうど間に来ると思いきや、やけに1/2の線に寄っているなぁ。(1/2の線の上に位置するのがそれ。）次は一応、2/3を計算してみるが、これも1/2の線に寄っている。あまりにも1/3と0/1の間があき過ぎなので、埋めるためにまずは1/4に挑戦するが、なんかやけに曲がってきた。次は1/5,1/6と計算してみるが、だんだん計算量が増えてきて計算時間がかなりかかる上に線が角張ってきた。この辺が限界か？
いずれにしても、想像以上にけったいな形に見えるが、これはどう解釈すべきか？誤差が集積してきているだけか、あるいは本質的にこのような姿なのか。

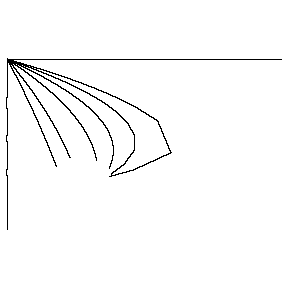
（見えている線は左の真っ直ぐ下向きな線から数えて、1/1, 2/3, 1/2, 1/3, 1/4, 1/5, 1/6, 0/1に対応するwordのトレース函数のreal locusである。1/5の線は誤差が大きすぎていびつになっている）
★それにしても、Mathematicaを起動するとその後はパソコンを一度再起動しないと他のソフトがまともに動かないのには困ったものだ。

1999年9月10日の記録

今月末には広島大学での学会でこの話題について発表しないといけないので、そろそろ真面目に絵を描くことを考えないといけないということで、3ヶ月ぶりにMathematicaを起動してみました。
で、今度は出来るだけ累積誤差を少なくするために最初から対応する行列のトレースを基本となるトレースの多項式で展開をしておいてから代入させるという方法を採ってみました。その結果描かせたreal locusが次の絵です。

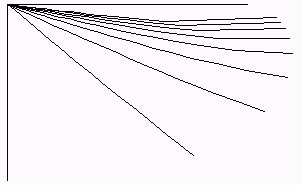
やはりどうも前に描かせたものは計算精度に問題があったのか、今回のはちゃんとinner pointing cuspがあるのが見えてきます。ちなみに、描かせたTeichmueller空間内のreal locusは下の方から順に AB, A²B, A³B, A⁴B, A⁵B, A⁶B, A⁷B, A⁸B, A⁹B, A に対応する元のモノドロミー表現のhyperbolic locus（のparabolicに向かう部分）になっています。（ちなみに、真っ直ぐ下に向かっているのがABに対応するもので、水平になっているものがAに対応するものです。前回とは記法が違いますが、前回の記法ではこれらは1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 0/1に対応していると言えるでしょう。）

なお、さらに広い範囲にわたって Aのモノドロミー像のトレースの虚部を3次元グラフ化したものが次の図です。大体、範囲としては|x|<10, |y|<10というところとお考え下さい。（少しずれているかもしれませんし、そもそも標準的な座標について説明していないのであまり意味がないかもしれませんが。）

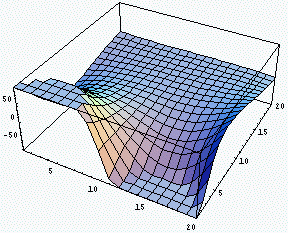
かなり複雑な挙動を示しています。さらに、このグラフの高さが正か負かで白黒に塗り分けたものが次の図です。メッシュが荒いので変になってしまっている部分もありますが、もう少し細かくすれば構造がより詳しく分かるのではないかと思います。いずれにしても、境界が交わっている部分は近くに分岐点があることを意味しています。分岐値がちょうど0になっているかどうかは分かりませんが、対称性から分岐値は実数になっているであろうと思われます。その値がいくらかは計算すれば分かると思いますが、今は何とも言えません。

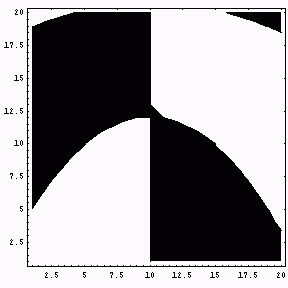
（どうも、一番最初に零点が見えると言っていたのは、A²のトレースを考えていたことに原因があったようです。2乗してしまうので、純虚になる部分まで見えてしまっていたようです。）

★それにしても、Mathematicaの引き起こす影響は面倒です。どうも、特定のキーを受け付けなくなってしまうようです。例えばEudoraなどではまともにメールが書けなくなってしまいます。原因は不明ですが、症状を改善するには立ち上げ直すしかないようです。

1999年9月11日の記録

続きとしてもう少し広い範囲で計算させてみたのが次です。もう少し時間があればもっと詳しく計算させてみたいのですが。

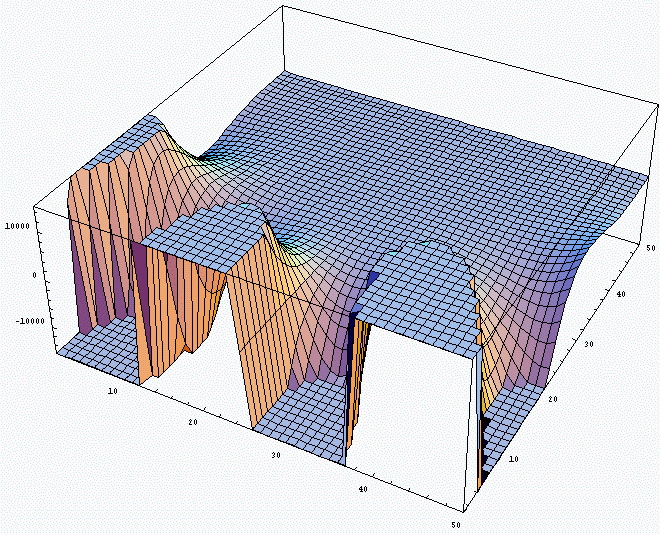
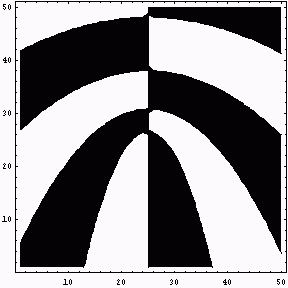
須川敏幸のホームページに戻る